프로그래머스 LV2 "멀리 뛰기"

프로그래머스 LV2 멀리 뛰기

기초부터 다시 공부를 하기위해 프로그래머스 라는 사이트에서 코딩테스트를 LV0 부터 가능한곳까지 못하는곳은 레퍼런스를 찾아가며 풀어보려고 합니다.

매일 1개의 풀이를 하고 그 풀이에대한 나의 생각 및 해석을 적어보려합니다.

오늘은 LV2 문제 ‘멀리 뛰기’ 문제입니다.

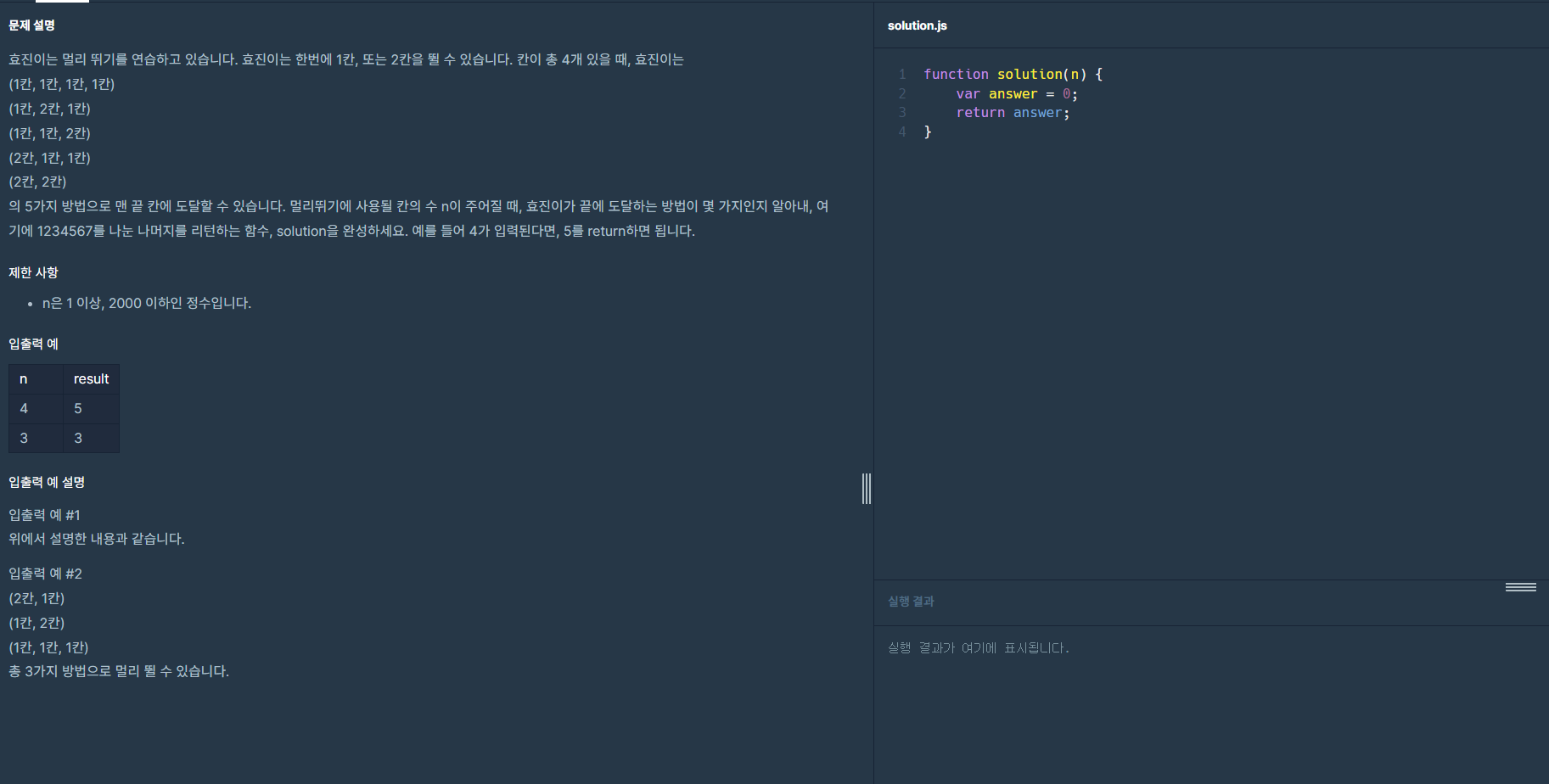
위 이미지가 프로그래머스 코딩문제입니다.

문제는 매개변수로 n이 주어지면 1과 2의 숫자로 조합해 몇가지 방법으로 나눌 수 있는지를 출력하는 문제입니다.

그럼 오늘의 문제를 한번 풀어보겠습니다.

기본 세팅 코드도 알아보겠습니다.

function solution(n) {
  var answer = 0;
  return answer;
}

기본 세팅 코드는 매개변수 n이 입력되고 함수 안에는 answer이라는 변수가 선언되어 리턴하는 간단한 기본 세팅 코드입니다.

이번문제는 피보나치 수열 문제에서 사용했던 방법으로 풀이가 가능할거같습니다.

이전 포스팅에서 다룬 피보나치 수열을 한번 더 복습해보겠습니다.

피보나치 수열

피보나치 수열(Fibonacci sequence)은 각 숫자가 앞의 두 숫자의 합으로 이루어진 수열을 말합니다. 예를 들어, 수열의 첫 번째와 두 번째 숫자는 각각 0과 1로 시작합니다. 그 다음부터는 이전 두 숫자의 합이 됩니다. 따라서 피보나치

수열은 다음과 같습니다: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

피보나치 수열을 구하는 방법은 여러 가지가 있습니다:

1. 재귀적 방법: 가장 직관적인 방법으로, 함수가 자기 자신을 호출하여 값을 계산합니다. 예를 들어, n번째 피보나치 수를 구하려면 n-1번째와 n-2번째 피보나치 수를 더하는 방식입니다. 하지만 이 방법은 중복 계산이 많아 비효율적입니다.

2. 메모이제이션을 사용한 재귀적 방법: 재귀적 방법의 비효율성을 개선하기 위해 이미 계산된 값을 저장해두고 필요할 때 다시 사용하는 방법입니다. 이를 통해 중복 계산을 피할 수 있습니다.

3. 반복적 방법: 반복문을 사용하여 피보나치 수를 계산하는 방법입니다. 이 방법은 변수 두 개를 사용하여 이전 두 값을 기억하고, 이를 이용해 다음 값을 계산합니다. 반복적 방법은 재귀적 방법보다 훨씬 효율적입니다.

4. 동적 계획법(Dynamic Programming): 이 방법은 배열을 사용하여 이전에 계산된 값을 저장하고, 이를 바탕으로 다음 값을 계산하는 방식입니다.

이렇게 피보나치 수열에 대해서 알아보았습니다.

그럼 오늘 문제의 풀이를 코드로 한번 작성해 보겠습니다.

function solution(n) {
    let arr = [1n, 1n, 2n];
    for(let i = 3; i <= n; i++) {
        arr.push(arr[i - 1] + arr[i - 2]);
    }
    return arr[n] % 1234567n;
}

위 코드의 간단한 설명을 알려드리겠습니다.

1. let arr = [1n, 1n, 2n];: 우선 첫 번째, 두 번째 항은 각각 1로 초기화되고, 세 번째 항은 2로 초기화됩니다. 이 배열은 이후 각 단계에서의 결과를 저장하는 데 사용됩니다.

2. for(let i = 3; i <= n; i++) {: 반복문을 사용하여 세 번째 항부터 n까지의 결과를 계산합니다. 초기값으로 i는 3부터 시작합니다.

3. arr.push(arr[i - 1] + arr[i - 2]);: 현재 단계에서의 결과를 배열에 추가합니다. 이전 단계와 그 전 단계의 결과를 더하여 현재 결과를 계산합니다. 이것이 피보나치 수열의 점화식입니다.

4. return arr[n] % 1234567n;: 계산된 결과를 배열에서 가져와서 1234567로 나눈 나머지를 반환합니다. 이는 문제에서 요구한 것과 동일합니다.

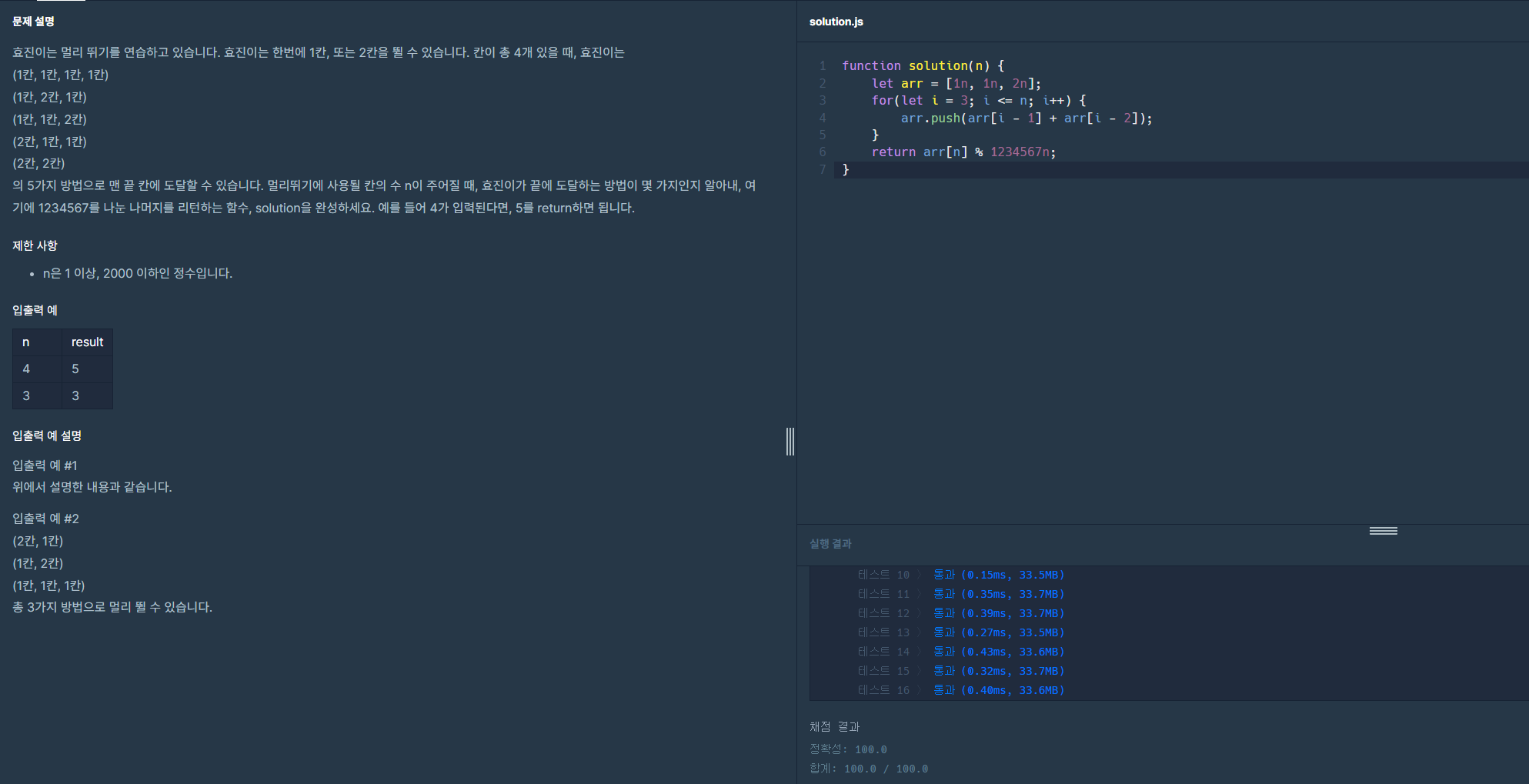
그럼 코드를 프로그래머스에 한번 확인해보겠습니다.

성공이네요!

오늘은 프로그래머스 LV2 ‘멀리 뛰기’ 문제의 대해서 알아봤습니다.

제 방법이 꼭 정답은 아니니 그저 이런방법도 있구나하고 참고용으로만 봐주시면 감사하겠습니다.

감사합니다.